1. A ti, 216 años después:

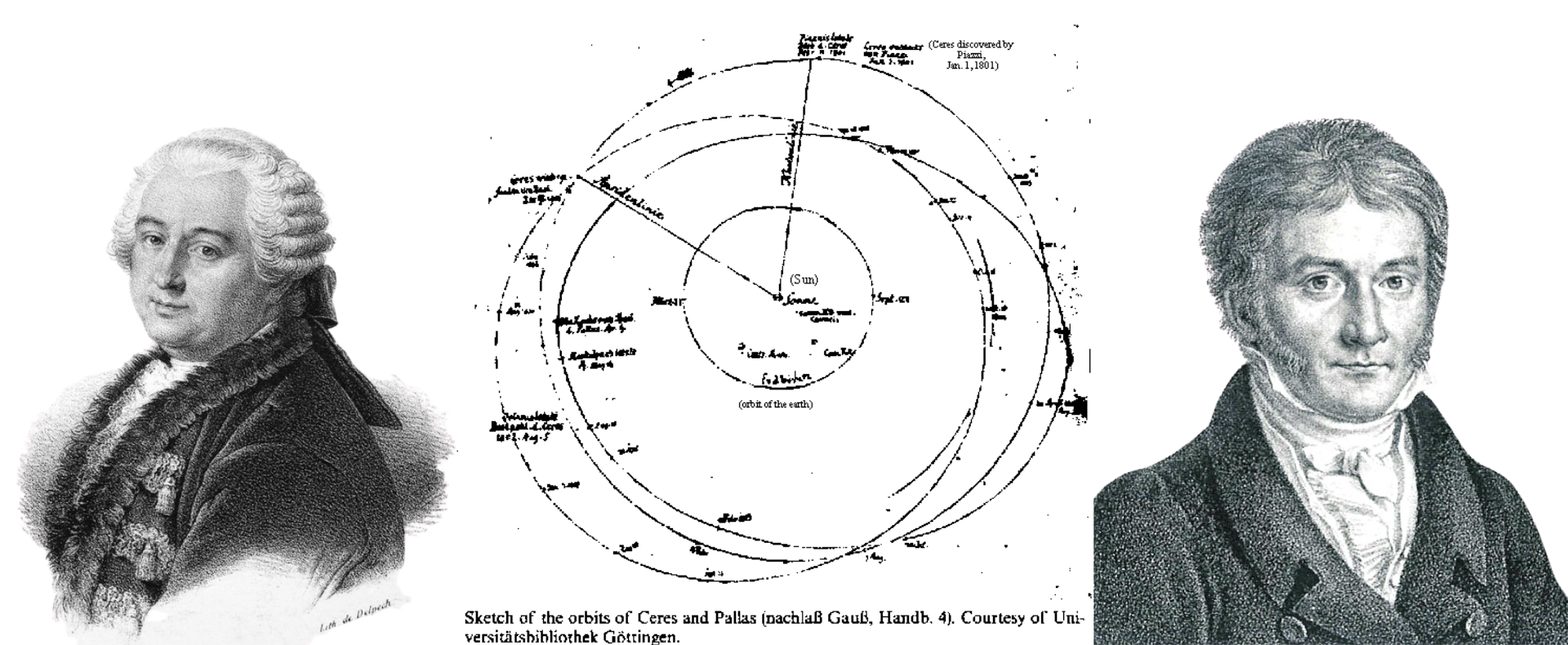
Hoy en clase de Métodos de Predicción Lineal, nuestro profesor nos ha presentado un breve recorrido histórico sobre la evolución de las técnicas empleadas en este campo, deteniéndose especialmente en un famoso rifirrafe entre dos grandes figuras: Carl-Friedrich Gauss el príncipe de los matemáticos, y el francés Adrien-Marie Legendre, a propósito de uno de los procedimientos más influyentes en la estadística y la astronomía: el método de los mínimos cuadrados.

2. El contexto histórico: finales del siglo XVIII

Isaac Newton (1643-1727) abrió la puerta a una nueva forma de entender el universo: sus leyes pusieron en marcha a generaciones de investigadores dispuestos a comprobar, con telescopios y cálculos, los principios que podían sostener el mundo. Décadas después de su muerte, con la mecánica newtoniana en vías de consolidarse, la mirada científica se centraba en confirmar aquellas teorías físicas a través del movimiento de los astros. Afinar las órbitas a partir de datos imperfectos permitía comprobar si las leyes de Newton describían fielmente la realidad o si, por el contrario, existían desviaciones que podían apuntar a fenómenos aún desconocidos.

3. ¿Cómo se medían las distancias a los astros en el siglo XVIII?

Dado que hace 200 años no tenían telemetría láser como la que usamos hoy en día para medir distancias dentro del Sistema Solar, los astrónomos recurrían a métodos geométricos y trigonométricos, aprovechando principios ópticos y las leyes de Newton y Kepler. Las técnicas clave eran:

1) Paralaje:

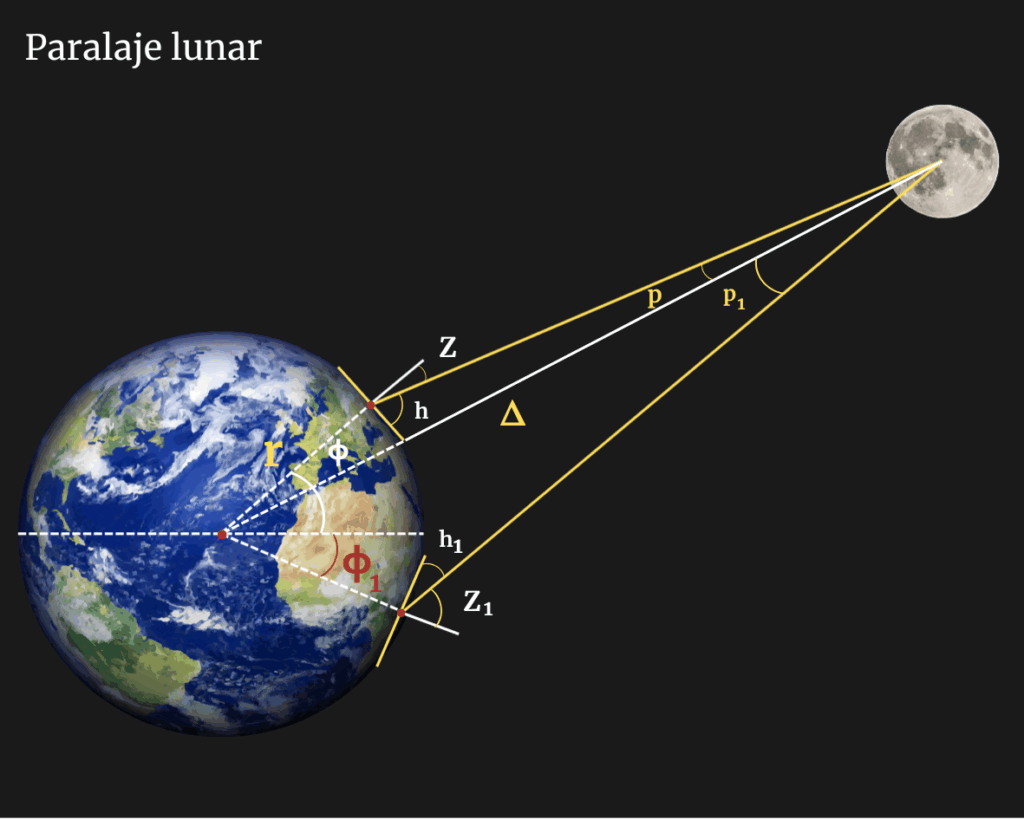
Se observaba el mismo astro desde dos puntos distintos de la Tierra (o en diferentes momentos, usando el movimiento de la Tierra en su órbita) y, a partir del ángulo de desviación aparente, se calculaba la distancia por trigonometría. Fue fundamental para medir distancias a la Luna (como he ilustrado en las fotos) y, más tarde, a planetas cercanos. De hecho he mencionado en anteriores artículos a Friedrich Bessel, matemático, astrónomo y primer hombre en determinar el paralaje de una estrella.

2) Tránsitos planetarios (Venus):

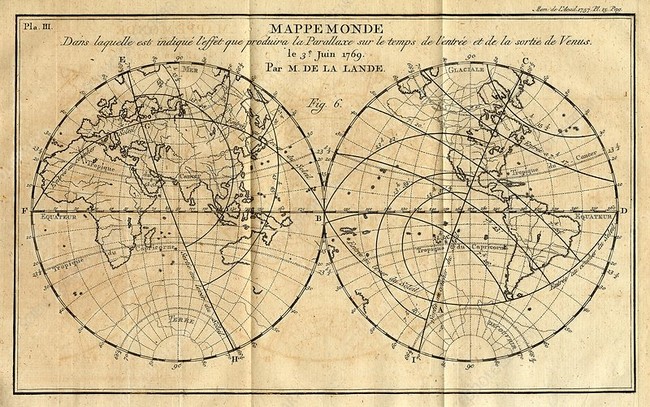
En especial, los tránsitos de Venus (cuando pasa por delante del disco solar). Al observarlos desde distintos lugares del globo, se podía calcular el paralaje solar y con ello estimar la distancia media Tierra-Sol (la Unidad Astronómica). Esta fue una de las grandes campañas científicas del siglo XVIII: los tránsitos de 1761 y 1769 movilizaron expediciones internacionales (Cook, Chappe d’Auteroche, entre otros).
Recomiendo encarecidamente este estudio del Centro Nacional de Información Geográfica:

Tránsitos: La medida del sistema solar y de otros sistemas planetarios

3) Aplicación de las leyes de Kepler y Newton:

Midiendo posiciones relativas (ángulos, tiempos, periodos orbitales), se podían deducir proporciones de distancias y tamaños de órbitas.
Newton mismo, en los Principia (1687), mostró cómo derivar relaciones de distancia a partir de periodos orbitales.
He encontrado en la página de la UPV unos recursos online sobre dinámica celeste en la que se explica muy bien la descripción del movimiento relativo del cuerpo y trata justamente de cómo se derivan relaciones de distancia a partir de los periodos orbitales, es decir, la tercera ley de Kepler puesta en términos relativos:

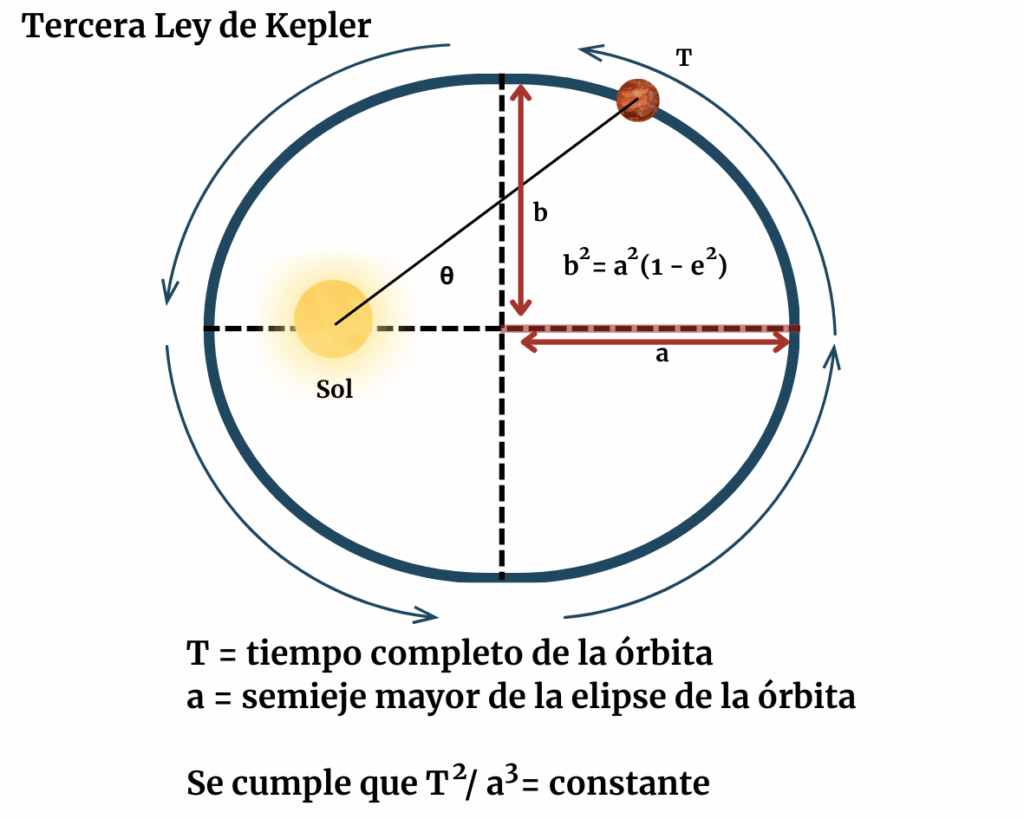
El valor absoluto (en km) llegó al combinar esta relación con mediciones de paralaje solar o de tránsitos de Venus, que dieron la escala real del Sistema Solar.

4. El desafío matemático del cambio de siglo: la órbita de Ceres

En 1801, el astrónomo italiano Giuseppe Piazzi descubrió un nuevo cuerpo celeste, al que denominó Ceres, entre Marte y Júpiter.
Piazzi solo pudo observar a Ceres durante 41 días, antes de que el cuerpo celeste se ocultara tras del sol. Para que los astrónomos pudieran volver a encontrar a Ceres y continuar con su estudio, era necesario calcular su órbita y predecir su futura posición en el cielo.

Leer más sobre Ceres y los planetas enanos (NASA)

5. Adrien-Marie Legendre

Adrien-Marie Legendre (1752-1833) fue un matemático francés de primer nivel, una figura clave en la transición entre el siglo XVIII y XIX.
En 1805 publicó su obra Nouvelles méthodes pour la détermination des orbites des comètes, donde presentó por primera vez de manera formal el método de los mínimos cuadrados (en la imagen 2, a continuación), méthode des moindres carrés, sin ligarlo a la probabilidad.
Legendre no participó en el famoso caso de la órbita de Ceres, su obra trataba de forma general de los cálculos de las órbitas de los cometas.

Obra original: Nouvelles méthodes pour la détermination des orbites des comètes

6. Carl Friedrich Gauss

Carl Friedrich Gauss (1777–1855), el príncipe de los matemáticos.
En 1795, con tan solo 18 años, Gauss afirmaba haber desarrollado de manera independiente el método de los mínimos cuadrados, aunque no lo publicó en ese momento. Lo aplicó por primera vez con éxito en el cálculo de la órbita del recién descubierto asteroide Ceres en 1801. Mientras otros métodos fracasaban en predecir su posición tras desaparecer detrás del Sol, las predicciones de Gauss, basadas en este procedimiento, resultaron extraordinariamente precisas y permitieron redescubrir el cuerpo celeste en diciembre del mismo año.
En 1809, Gauss publicó su obra mayor en astronomía, Theoria motus corporum coelestium, donde incluyó no solo el método de los mínimos cuadrados, sino también una justificación matemática rigurosa a partir de la teoría de la probabilidad. Fue allí donde declaró haberlo usado desde 1795, reforzando su reivindicación de prioridad frente a Legendre.

“Por lo demás, nuestro principio, que hemos utilizado desde el año 1795, ha sido publicado recientemente también por el ilustre Legendre en su obra Nouvelles méthodes pour la détermination des orbites des comètes, París, 1806…”

Con esta afirmación, Gauss daba a entender que había llegado al método antes de la publicación de Legendre, aunque nunca lo hubiera difundido. Esa expresión, “nuestro principio”, fue interpretada por Legendre como un intento de apropiarse de la prioridad, y marcó el inicio abierto de la controversia.

Obra original: Theoria motus corporum coelestium

7. La disputa

«Principium nostrum» o Gauss utilizando el plural mayestático…
Esta afirmación molestó profundamente a Legendre, que defendía que la prioridad debía otorgarse siempre al primero en publicar, y no al que alegaba haber usado un método sin pruebas impresas, incluso si esa persona era el mismísimo Gauss.
Primero lo expresó en una carta privada a Gauss en 1809, y más tarde, con mayor firmeza, en una nota añadida al suplemento de 1820 de su obra, donde lo acusaba abiertamente de atribuirse descubrimientos ajenos y recordaba que algo similar había sucedido con la ley de reciprocidad cuadrática (un teorema fundamental de la teoría de números que establece una relación entre la solubilidad de dos ecuaciones de congruencia cuadrática), enunciada por Euler en 1754, formulada por él en 1785 y demostrada rigurosamente por Gauss en 1801.
Gauss, por su parte, nunca respondió públicamente al ataque de Legendre, pero en su correspondencia privada reafirmó que había usado el método desde la década de 1790 y que varios astrónomos como Olbers o Lindenau podían dar fe de ello.
Heinrich Wilhelm Olbers (descubridor de Palas en 1802) y Bernhard von Lindenau estuvieron entre los astrónomos que intentaron calcular sin éxito la órbita de Ceres usando los métodos tradicionales de la época (aproximaciones geométricas y ajustes manuales).

8. El desenlace

Con el tiempo, la historiografía matemática zanjó el debate de forma más o menos equilibrada: Legendre fue el primero en publicar el método, mientras que Gauss fue quien lo dotó de una fundamentación matemática sólida y lo consolidó como herramienta indispensable en astronomía y estadística.

¿En qué consiste exactamente el método de los mínimos cuadrados?

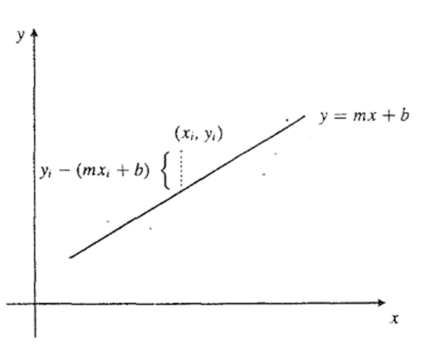
El método de los mínimos cuadrados ajusta un modelo lineal a datos eligiendo los parámetros que minimizan la suma de los errores al cuadrado entre lo observado y lo predicho (proyecta los datos sobre el espacio generado por los predictores). Con ello obtiene estimaciones estables y, bajo supuestos habituales, óptimas entre las lineales e insesgadas.

Un repaso más exhaustivo sobre el MCO: bibliografía de la Universidad de Sevilla.

9. Para ti, dentro de 216 años:

Lo que entonces estuvo marcado por una disputa de prioridad con Legendre terminó convirtiéndose en la lengua franca de la predicción lineal: una idea sencilla —proyectar los datos sobre el espacio generado por los predictores— que sostiene desde la astrometría y la geodesia hasta la econometría, la calibración de sensores y el aprendizaje automático. No solo es una reliquia histórica, sino también una herramienta de uso diario. Llega a las manos de estudiantes como yo en las primeras asignaturas de la carrera y nos acompaña cada vez que ajustamos una recta, validamos un modelo o estimamos un efecto.
He ahí el arco de esta historia: del choque de firmas a una idea que, 216 años más tarde (a octubre de 2025) continúa trazando líneas de sentido sobre el mundo.