
La media siempre ha sido el «hijo favorito» de la estadística, un estimador ideal, elegante y eficiente. Si nos apetece estudiar la altura de una población, el rendimiento de una máquina o incluso la posición de un astro, bastaba con sumar las observaciones y dividirlas por el total. Es prácticamente un punto de equilibrio perfecto, el estimador de máxima verosimilitud que nos entrega la verdad desnuda de los datos sin sesgos ni artificios.
Charles Stein, en 1965 cometió el equivalente a una herejía estadística: destronó la media como mejor estimador para una situación extremadamente común, tachando el uso de este «hijo favorito» de inadmisible (literalmente).
Cabe recalcar que la inadmisibilidad en el contexto matemático no significa que esté prohibido por ley usar ese método, sino que simplemente hay uno mejor, que usualmente da menos errores.
Stein clavó una estaca en la intuición de las personas al demostrar que en el momento en el que intentamos medir 3 o más cosas al mismo tiempo, la media se vuelve inadmisible: el camino más corto hacia la precisión no es confiar ciegamente en cada dato individual, sino contaminar deliberadamente nuestras mediciones con la información de las demás.
Un hallazgo contraintuitivo: la paradoja de Stein
El enunciado matemático formal establece que, cuando se intentan estimar simultáneamente tres o más parámetros independientes (como las medias de distintos grupos) bajo una distribución normal, el estimador tradicional de la media muestral es inadmisible. Esto significa que, aunque la media parece el cálculo más lógico, existe un estimador alternativo (el de James-Stein) que garantiza un error cuadrático medio menor de manera universal.
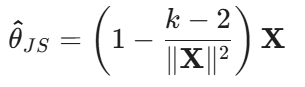
(En la práctica se suele usar la versión «parte postiva», para evitar que el factor encogimiento se vuelva negativo)
Mediante la aplicación de un factor de encogimiento, este método corrige el ruido aleatorio de las observaciones individuales al atraerlas hacia un centro común, demostrando que en dimensiones altas (k > 3), la precisión global del sistema aumenta si se sacrifica la exactitud individual de cada dato.
Contaminar los datos con otros funciona porque el azar es «ruidoso» y desordenado. Al obligar a los datos a compartir información, el ruido de uno se cancela con el ruido de otro, dejan al descubierto la señal real que subyace en el conjunto.
La media falla a partir de la tercera dimensión: el fenómeno de la fuga de magnitud
Para explicar bien este concepto hay que abandonar la aritmética simple y pensar dentro de la geometría espacial.
Si estamos tratando de dar en el blanco de una diana, nuestro objetivo será el centro (llamémoslo θ), pero debido al azar (ruido), nuestros flechazos van a caer al rededor de este centro θ.
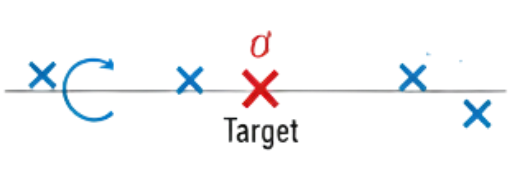
Si solo estamos teniendo en cuenta una dimensión (una línea), nuestro margen de error está muy confinado, solo nos vamos a poder equivocar de derecha a izquierda.
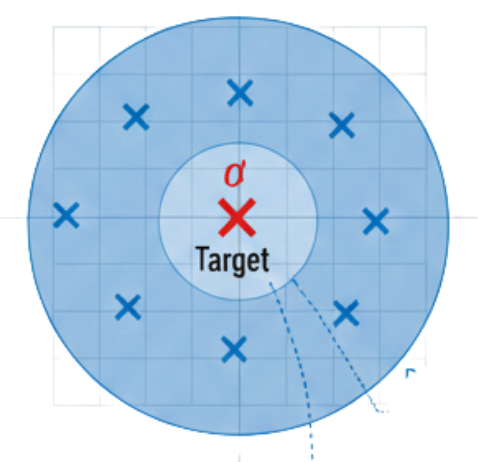
Con dos dimensiones (un plano x-y) nuestro error se extrapola a cualquier dirección dentro del círculo.
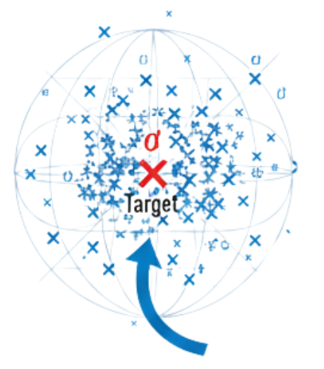
Cuando pasamos a 3 dimensiones (tres distintos temas a estudiar), el espacio disponible para alejarse del centro crece de forma explosiva (se transforma en una una esfera).
Explicación geométrica:
El error total de nuestro estimador es la suma de los cuadrados de los errores individuales. Si tenemos k dimensiones, el error total (la distancia al cuadrado desde nuestra estimación al valor real) es:
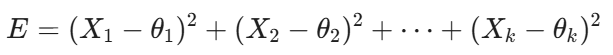
A medida que vamos añadiendo más dimensiones, se va sumando más fuentes de error positivo. En 1D o 2D, la probabilidad de que el vector de datos X sea una representación fiel de θ es alta. Pero a partir de k=3, el vector observado tiende a ser sistemáticamente más largo que el vector real de las medias.
Debido a la geometría del espacio euclídeo, en 3D el «ruido» que mencionaba antes, tiende a empujar los datos hacia afuera del centro con más fuerza de la que los mantiene cerca. Los datos observados están, casi siempre, demasiado lejos de origen (nuestro blanco en la diana).
Stein se dio cuenta de que en tres dimensiones, el estimador de máxima verosimilitud (la media) sufre de un exceso de confianza (da por hecho que los valores extremos son reales cuando en realidad muchas veces son producto del ruido expandido en el espacio tridimensional).
Si se multiplica el vector por un factor menor que 1 (el encogimiento) lo que estamos haciendo es reconocer que la magnitud del vector observado es probablemente exagerada, y «encoger» el vector de vuelta hacia una zona con mayor probabilidad.
El factor de encogimiento de James-Stein en 1 y 2 dimensiones no funciona, para k=1 el factor es negativo o directamente pierde sentido la reducción de riesgo y para k=2 el término se anula. Solo cuando k es mayor o igual 3, el beneficio de reducir la varianza (al encoger) es mayor que el daño de introducir un sesgo.
Stein no «rompió la estadística», simplemente nos demostró que, a partir de la tercera dimensión, la intuición es el estimador más costoso de todos.